Introduction:
One of the few scientific fields fortunate enough to have a distinct beginning is Information Theory; Claude Shannon's 1948 paper evolved from being a single theoretical paper into a broad field that has redefined our world. We have been provided the opportunity to study the social, political, and technological interactions that have helped guide its development and define its trajectory, and has given us insight into how a new field evolves.
Research was primarily theoretical in the beginning, with little perceived applications. Christensen said that usually an innovator's dilemma is that he cannot garner support for his novel ideas because he cannot always promise an end profit. Fortunately, Information Theory was sponsored in anticipation of what it could provide. This perseverance and continued interest eventually resulted in the multitude of technologies we have today.
“Before 1948, there was only the fuzziest idea of what a message was. There was some rudimentary understanding of how to transmit a waveform and process a received waveform, but there was essentially no understanding of how to turn a message into a transmitted waveform.”
[Gallager, Claude Shannon: A Retrospective, 2001]
Information Theory:
In 1948, Shannon published his seminal paper “A Mathematical Theory of Communication” in the BellSystems Technical Journal. He showed how information could be quantified with absolute precision, and demonstrated the essential unity of all information media. Telephone signals, text, radio waves, and pictures, essentially every mode of communication, could be encoded in bits. This unimaginable idea provided a “blueprint for the digital age”
One of the basic postulates of Shannon's Information Theory is that information can be treated like any measurable physical quantity, such as mass or volume.
The basic elements of any general communications system include
- a source of information which is a transmitting device that transforms the information or "message" into a form suitable for transmission by a particular means.
- the means or channel over which the message is transmitted.
- a receiving device which decodes the message back into some approximation of its original form.
- the destination or intended recipient of the message.
- a source of noise (i.e., interference or distortion) which changes the message in unpredictable ways during transmission.
One must note that the concept "information" as understood in information theory is not associated with any inherent meaning in a message. It is rather a degree of order, or non-randomness, that can be measured and treated mathematically much as mass or energy or other physical quantities. A mathematical characterization of the generalized communication system yields a number of important quantities, including
- the rate at which information is produced at the source.
- the capacity of the channel for handling information.
- the average amount of information in a message of any particular type.
The techniques used with information theory are, to a large extent, drawn from the concepts of probability. The accuracy of any transmission of information under given conditions of noise interference, for example, are estimated probabilistically, as are the numerous approaches to encoding and decoding that have been developed to reduce the uncertainty or error to minimal levels.
Uncertainty:
Information and Uncertainty are elements of any process that selects one or more objects from a set of objects. An attempt is made in the following few paragraphs to explain these terms with the help of an example.
Suppose we have a device that can produce 3 symbols, A, B, or C. As we wait for the next symbol, we are uncertain as to which symbol it will produce. Once a symbol appears and we see it, our uncertainty decreases, and we remark that we have received some information. That is, information is a decrease in uncertainty.
How should uncertainty be measured? The simplest way should be to say that we have an "uncertainty of 3 symbols". This would work well until we begin to watch a second device at the same time, which, let us imagine, produces symbols 1 and 2. The second device gives us an "uncertainty of 2 symbols". If we combine the devices into one device, there are six possibilities, A1, A2, B1, B2, C1, C2. This device has an "uncertainty of 6 symbols". This is not the way we usually think about information, for if we receive two books, we would prefer to say that we received twice as much information than from one book. That is, we would like our measure to be additive.
Entropy:
Entropy is a quantitative measure of the disorder of a system and inversely related to the amount of energy available to do work in an isolated system. The more energy has become dispersed, the less work it can perform and the greater the entropy.
The Shannon entropy equation provides a way to estimate the average minimum number of bits needed to encode a string of symbols, based on the frequency of the symbols.
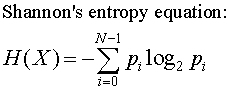
In the Shannon entropy equation, pi is the probability of a given symbol.
The minimum average number of bits is per symbol is
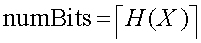
If we have a symbol set {A,B,C,D,E} where the symbol occurance frequencies are:
A = 0.5 B = 0.2 C = 0.1 D = 0.1 E = 0.1
The average minimum number of bits needed to represent a symbol is
H(X) = -[(0.5log20.5 + 0.2log20.2 + (0.1log20.1)*3)
H(X) = -[-0.5 + (-0.46438) + (-0.9965)]
H(X) = -[-1.9]
H(X) = 1.9
Rounding up, we get 2 bits/per symbol. To represent a ten character string AAAAABBCDE would require 20 bits if the string were encoded optimally. Such an optimal encoding would allocate fewer bits for the frequency occuring symbols (e.g., A and B) and long bit sequences for the more infrequent symbols (C,D,E).
References:
[1] Aftab, Cheung, Kim, Thakkar, Yeddanapudi; Information Theory: Information Theory And The Digital Age
[2] http://www.nyu.edu/pages/linguistics/courses/v610003/shan.html
[3] Ian Kaplan (2002):http://www.bearcave.com/misl/misl_tech/wavelets/compression/shannon.html
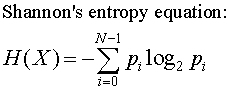
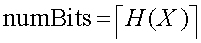
No comments:
Post a Comment