COLLECTIVE BEHAVIOUR OF STOCK PRICE MOVEMENTS IN AN EMERGING MARKET

Financial markets can be considered as complex systems having many interacting elements and exhibiting large fluctuations in their associated observable properties, such as stock price or market index. The state of the market is governed by interactions among its components, which can be either traders or stocks. In addition, market activity is also influenced significantly by the arrival of external information like state of other markets, price of different commodities etc.

The data is taken from National Stock Exchange (NSE) which is an emerging market. The data analysed was the closing price data of 201 stocks of  for 2607 days. To observe correlation between the price movements of different stocks, we first measure the price fluctuations such that the result is independent of the scale of measurement.

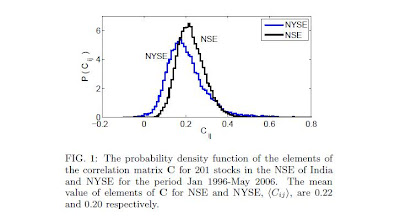
If P_i(t) is price of the stock i = 1, . . . ,N at time t, then the normalised price return r_i(t, Δt) of the i^th stock over a time interval  Δt is defined as

Equal time cross-correlation(measure of similarity of 2 waveforms as a function of a time-lag applied to one of them) matrix C, whose element C_ij represents the correlation between returns for stocks i and j, was calculated. It was found that the correlation among stocks in NSE is larger on the average compared to that among the stocks in New York Stock Exchange (NYSE) which is a developed market. (Fig 1).

A. Eigenvalue spectrum of correlation matrix

If the N return time series of length T are mutually uncorrelated, then the resulting random correlation matrix is called a Wishart matrix. In the limit N → ∞, T → ∞, such that Q ≡ T/N ≥ 1, the eigenvalue distribution of this random correlation matrix is given by

In the NSE data, there are N = 201 stocks each containing T = 2606 returns; as a result Q = 12.97. Therefore, in the absence of any correlation among the stocks, the eigenvalue distribution P(λ) should be bounded between λ_min = 0.52 and λ_max = 1.63. But a few of the largest eigenvalues deviate significantly from the RMT(Random Matrix theory)  bound (Fig. 2). The number of these deviating eigenvalues is relatively few for NSE compared to NYSE.

B. Properties of ‘Deviating’ Eigenvalues

The largest eigenvalue λ₀ is indicative of a common factor that affects all the stocks with the same bias, the largest eigenvalue is associated with the market mode, i.e., the collective response of the entire market to external information. The eigenvalues occurring in the range predicted by RMT denote the noise in the sampled data and doesn’t contribute to the market characteristics. Of more interest for understanding the market structure are the intermediate eigenvalues, i.e., those occurring between the largest eigenvalue and the bulk of the distribution predicted by RMT. Each of these eigenvalues corresponds to a related group of stocks. 

C. Filtering the correlation matrix

We now use a filtering method to remove market mode, as well as the random noise . The correlation matrix is first decomposed as

Where λ_i are the eigenvalues of C sorted in descending order and u_i are corresponding eigenvectors. The contribution of the intra-group correlations to the C matrix can be written as a partial sum of λ_ku_ku_k^T , where k is the index of the corresponding eigenvalue. Thus, the correlation matrix can be decomposed into three parts, corresponding to the market, group and random components:

The Group Correlation Matrix is used to construct the network of interacting stocks. The adjacency matrix A of this network is generated from the group correlation matrix C group by using a threshold cth such that Aij = 1 if C^groupij > cth, and Aij = 0 otherwise. Thus, a pair of stocks are connected if the group correlation coefficient C^groupij is larger than a preassigned threshold value, cth. To determine an appropriate choice of cth = c* the number of isolated clusters was observed (a cluster being defined as a group of connected nodes in the network for a given cth ,a single node is ignored and not counted as a cluster) . For c* = 0.09, the largest number (3) of isolated clusters of stocks are obtained whereas the largest number of clusters obtained from NYSE data is greater than 3. From these 3 clusters, only two business sectors can be properly identified, namely the Technology and the Pharmaceutical sectors. 

The fact that the majority of the NSE stocks cannot be arranged into well-segregated groups reflecting business sectors leads to conclusion that intra-group interaction is much weaker than the market-wide correlation in the NSE. Most of the observed correlation among stocks is found to be due to effects common to the entire market, whereas correlation due to interaction between stocks belonging to the same business sector are weak. Emergence of an internal structure comprising multiple groups of strongly coupled components is a signature of market development.

Sources: Collective behavior of stock price movements in an emerging market(Raj Kumar Pan, Sitabhra Sinha)